The Dirichlet Hyperbola Method

07 Mar 2019

• analytic number theory

Recently, I had to use a classical number theory estimate for my undergrad thesis. By pure coincidence, I ran into my batchmates Jessica and James revising for an analytic number theory class, and they taught me exactly the method I needed. In this post, we go through the Dirichlet hyperbola method for estimating certain sums of arithmetic functions.

Suppose we want to find the number of integer lattice points in the first quadrant under the hyperbola $xy=N$, ie. the size of the set

$$S_N\coloneqq\{(x,y)\in\bb Z^2\,:\,x,y>0,\,xy\leq N\},$$

We could try to estimate this directly:

$$\begin{aligned} |S_N|&=\sum_{x\leq N}\sum_{xy\leq N}1\\ &=\sum_{x\leq N}\left\lfloor\frac Nx\right\rfloor\\ &=\sum_{x\leq N}\left(\frac Nx+O(1)\right)\\ &=N\log N+O(N). \end{aligned}$$

However, note that this estimate is not very tight. For instance, for $\frac N2\leq n\leq N$, we know that the summand is exactly $1$, but we are still incurring $O(1)$ error every term.

For a sharper estimate, we truncate the sum at some $1\leq u\leq N$, and estimate the remainder:

$$|S_N|=\sum_{x\leq u}\sum_{xy\leq N}1+\sum_{u< x\leq N}\sum_{xy\leq N}1.$$

As before, the first sum is equal to

$$\begin{aligned} \sum_{x\leq u}\sum_{xy\leq N}1&=\sum_{x\leq u}\left\lfloor\frac Nx\right\rfloor\\ &=\sum_{x\leq u}\left(\frac Nx+O(1)\right)\\ &=N(\log u+\gamma)+O(u). \end{aligned}$$

Here we have used the sharper asymptotic

$$\sum_{x\leq u}\frac1x=\log u+\gamma+O\left(\frac1u\right).$$

Write $v=N/u$. Then note that we have the disjoint union

$$\begin{aligned} S_n\cap\{y\leq v\}&=(S_n\cap\{u< x\leq N\})\\ &\quad\sqcup(S_n\cap\{x\leq u,\,y\leq v\}). \end{aligned}$$

Hence the second sum is equal to

$$\begin{aligned} \sum_{u< x\leq N}\sum_{xy\leq N}1&=\sum_{y\leq v}\sum_{xy\leq N}1-\sum_{y\leq v}\sum_{x\leq u}1\\ &=\sum_{y\leq v}\left\lfloor\frac Ny\right\rfloor-\lfloor v\rfloor\lfloor u\rfloor\\ &=\sum_{y\leq v}\left(\frac Ny+O(1)\right)-uv+O(u)+O(v)\\ &=N(\log v+\gamma)-N+O(u)+O(v). \end{aligned}$$

Putting these estimates together, we have

$$|S_N|=N\log u+N\log v+(2\gamma-1)N+O(u+v).$$

To minimise the error, we take $u=v=\sqrt N$, to finally obtain

$$|S_N|=N\log N+(2\gamma-1)N+O(\sqrt N).$$

The hyperbola method

More generally, we can apply the same method to sum certain arithmetic functions.

Recall that the convolution of two functions $g,h:\bb Z_{>0}\to\bb R$ is defined by

$$(g* h)(n)=\sum_{d|n}g(d)h\left(\frac nd\right).$$

Suppose that we want to estimate the asymptotic growth of the partial sums $\sum_{n\leq N}f(n)$. Now if we can write $f=g* h$ for some $g,h$, then we have

$$\begin{aligned} \sum_{n\leq N}f(n)&=\sum_{n\leq N}\sum_{x|n}g(x)h\left(\frac nx\right)\\ &=\sum_{n\leq N}\sum_{xy=N}g(x)h(y)\\ &=\sum_{xy\leq N}g(x)h(y). \end{aligned}$$

Now define the partial sums $G(n)=\sum_{x\leq n}g(x)$ and $H(n)=\sum_{x\leq n}h(x)$. For any choice of $u,v\geq0$ with $uv=N$, the trick in the previous section gives

$$\begin{aligned} \sum_{n\leq N}f(n)&=\sum_{xy\leq N}g(x)h(y)\\ &=\sum_{x\leq u}\sum_{xy\leq N}g(x)h(y)+\sum_{u< x\leq N}\sum_{xy\leq N}g(x)h(y)\\ &=\sum_{x\leq u}g(x)\sum_{y\leq N/x}h(y)+\sum_{y\leq v}h(y)\sum_{x\leq N/y}g(x)-\sum_{y\leq v}\sum_{x\leq u}g(x)h(y)\\ &=\sum_{x\leq u}g(x)H\left(\frac Nx\right)+\sum_{y\leq v}h(y)G\left(\frac Ny\right)-G(u)H(v). \end{aligned}$$

This identity is known as the Dirichlet hyperbola method, since it depends on a certain partition of the lattice points under the hyperbola $xy=N$. This is best seen with the help of the following picture; the three terms in the last line above are represented by the blue, red, and purple areas respectively.

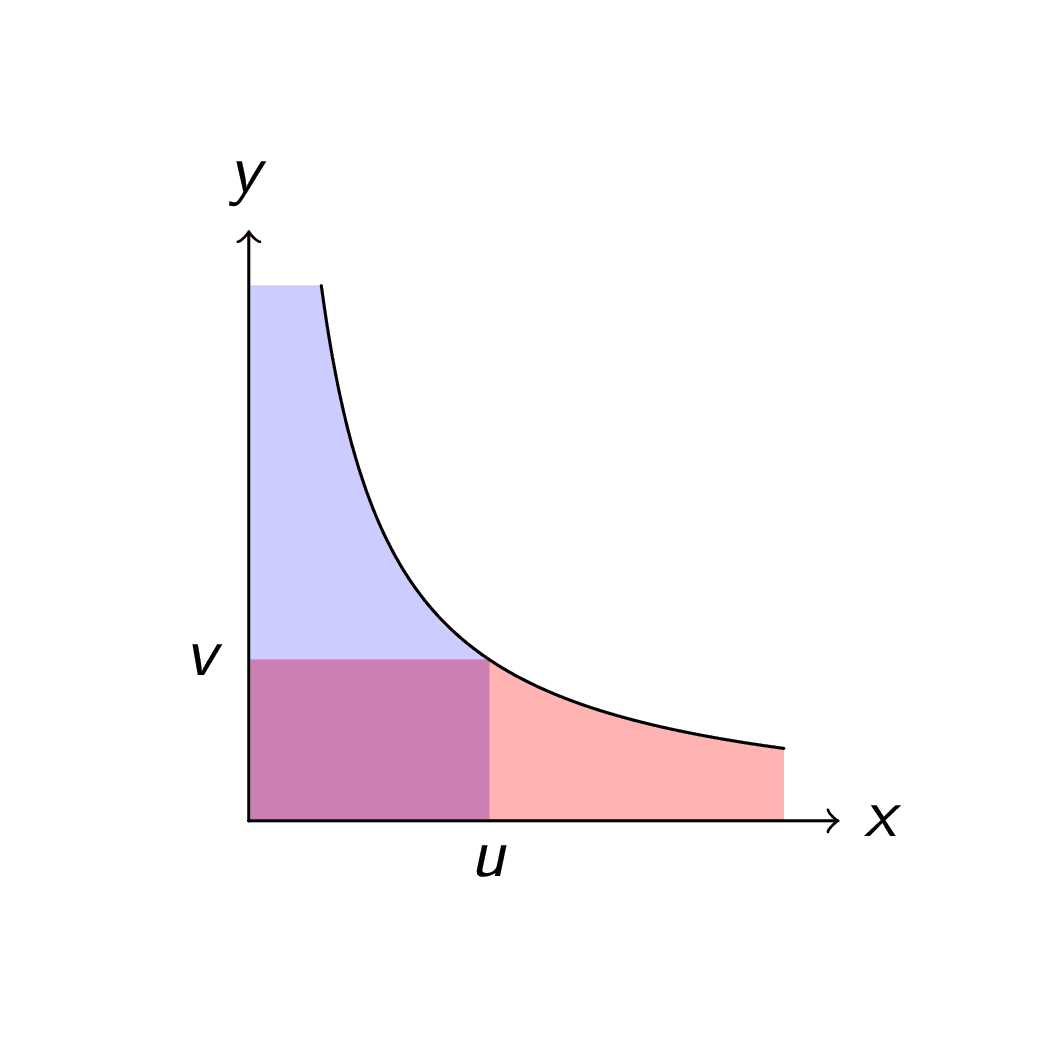
The example we gave in the previous section is the case when $g\equiv h\equiv1$. In this case, we have $f=1* 1=d$, the number-of-divisors function (sometimes written $\tau$). Hence we can interpret the result as the asymptotic for the partial sums of the number-of-divisors function,

$$\boxed{\sum_{n\leq N}d(n)=N\log N+(2\gamma-1)N+O(\sqrt N).}$$

More examples

Let $\sigma$ be the sum-of-divisors function. Note that $\sigma=\Id* 1$, where $\Id$ is the identity function $\Id(n)=n$. By the Dirichlet hyperbola method, we have

$$\begin{aligned} \sum_{n\leq N}\sigma(n)&=\sum_{x\leq u}x\left\lfloor\frac Nx\right\rfloor\\&\quad+\sum_{y\leq v}\frac{\lfloor\frac Ny\rfloor(\lfloor\frac Ny\rfloor+1)}2\\&\quad-\frac{\lfloor u\rfloor(\lfloor u\rfloor+1)}2\lfloor v\rfloor\\ &=\sum_{x\leq u}[N+O(x)]\\&\quad+\sum_{y\leq v}\left[\frac12\left(\frac Ny\right)^2+O\left(\frac Ny\right)\right]\\&\quad-\frac{Nu}2+O(uv+u^2)\\ &=Nu+O(N+u^2)\\&\quad+\frac12N^2\left(\zeta(2)+O\left(\frac1v\right)\right)+O(N\ln v)\\&\quad-\frac{Nu}2+O(N+u^2)\\ &=\frac{\zeta(2)}2N^2+O(Nu+N\ln v). \end{aligned}$$

By some experimentation, we see that we cannot do better than setting $u=1$, $v=N$, which yields

$$\boxed{\sum_{n\leq N}\sigma(n)=\frac{\zeta(2)}2N^2+O(N\ln N).}$$

For another example, we will compute the asymptotic for partial sums of $\varphi$, the Euler totient function. It is well-known that $\varphi* 1=\Id$ (proof sketch: consider the denominators of the fractions $\{\frac1n,\frac2n,\ldots,\frac nn\}$ when reduced to lowest terms), so by Möbius inversion we have $\varphi=\Id* \mu$, where $\mu$ is the Möbius function. We now apply the Dirichlet hyperbola method with $u=1^-$, $v=N^+$ to obtain

$$\begin{aligned} \sum_{n\leq N}\varphi(n)&=\sum_{y\leq N}\mu(y)\frac{\lfloor\frac Ny\rfloor(\lfloor\frac Ny\rfloor+1)}2\\ &=\sum_{y\leq N}\mu(y)\left(\frac12\left(\frac Ny\right)^2+O\left(\frac Ny\right)\right)\\ &=\frac12N^2\left(\sum_{y=1}^\infty\frac{\mu(y)}{y^2}-O\left(\frac1N\right)\right)+O(N\ln N)\\ &=\frac C2N^2+O(N\ln N), \end{aligned}$$

where it remains to compute the sum

$$C\coloneqq\sum_{y=1}^\infty\frac{\mu(y)}{y^2}.$$

By Möbius inversion, we know that $\mu* 1=\delta$, where

$$\delta(n)=\begin{cases}1,&\text{if }n=1\\0,&\text{else}.\end{cases}$$

Now by the theory of Dirichlet series, we have

$$\left(\sum_{n=1}^\infty\frac{\mu(n)}{n^s}\right)\left(\sum_{n=1}^\infty\frac1{n^s}\right)=\sum_{n=1}^\infty\frac{\delta(n)}{n^s}=1,$$

valid for all $\Re(s)>1$. Hence

$$\sum_{n=1}^\infty\frac{\mu(n)}{n^s}=\frac1{\zeta(s)},$$

so $s=2$ gives $C=\frac1{\zeta(2)}$. Hence

$$\boxed{\sum_{n\leq N}\varphi(n)=\frac1{2\zeta(2)}N^2+O(N\ln N).}$$